Mathematical Expressions

This chapter clarifies a unified style to render mathematical symbols and formula in Espressif documentation. It covers key components of mathematical expressions, along with conventions on spacing, font, typesetting and citing formulas.

Key Components

Mathematical expressions often involve various components such as variables, constants, operators, and formulas etc. Here is an overview of the key components in mathematical expressions.

Key Components
Components	Definition	Example
Variable	A symbol (often a letter) representing quantity that can change or vary.	x (could denote position) t (might represent time)
Constant	A symbol that has a fixed value.	π = 3.14159 e = 2.718
Physical Quantity	A product of a numerical value (a pure number) and a unit.	length mass
Operator	A symbol that represents a mathematical operation.	±, =, ∩, ∫, Π, Σ
Enclosing Mark	A pair of symbols that control the order of operations.	parentheses brackets braces
Formula	An expression that calculates a specific value or relationship between variables.	A = \(πr^2\) \[\mathrm{UART}\_{\mathrm{CLKDIV}} + \frac{\mathrm{UART}\_{\mathrm{CLKDIV\_FRAG}}}{16}\]
Equation	A mathematical expression that contains the “=”.	f(x) = y
Inequality	A mathematical expression where we compare two expressions that are not equal by using the symbols such as < > = ≥ ≤ ≠.	x < 1

Note

Define all symbols for mathematical constants, variables, and unknown quantities the first time you use them in the text. Do not define standard mathematical constants such as π, i, and e.

Spacing

The general consideration is good mathematical spacing helps to indicate grouping: Things that are more closely related should be set more tightly than things that are less closely related. Please see the following spacing convention with examples.

Leave a space
- before and after mathematical signs used as operators (=, ≠, ≈, ≅, >, <, +, –, ×, ÷, etc., but not slash, ratio colon, or centered dot), except when they appear in superscripts or subscripts
  
  Example
  
  LEDC_CLK_DIV = \(A + \frac{B}{256}\)
- before and after trigonometric
  
  Example
  
  \(4 \sin \theta\)
  
  Leave a space before and after sin.
- before and after functions that are set in roman type when their arguments are not in enclosing marks
  
  Example
  
  \(1 + \log {\mathrm{y}}\)
  
  Leave a space before and after log.
Leave no space
- between single-item variables being multiplied
  
  Example
  
  xy
- in any part of a superscript or subscript, unless confusion or misreading would result
  
  Example
  
  \(E_{\mathit{λ}>353}\)
  
  Leave no space before and after >.
- between any character and its own superscript, prime, or subscript
  
  Example
  
  \(\mathit{x}^{\mathit{a+b}}\)
  
  Leave no space between x and a.
- on either side of a colon used for a ratio
  
  Example
  
  1:10
- on either side of a centered dot used for multiplication
  
  Example
  
  \(W = F \cdot d\)
  
  Leave no space before and after ⋅. The formula contains three physical quantities: W represents work, as the product of force (F) and distance (d).
- on either side of a slash used for division
  
  Example
  
  \(\mathit{a}/\mathit{b}\)
- after mathematical operators used as adjectives
  
  Example
  
  –2 °C
  
  Leave no space after –.
- after functions when the argument is in parentheses
  
  Example
  
  \(\tan(π/4)\)
  
  Leave no space after tan.
- between an opening parenthesis, bracket, or brace and the next character
  
  Example
  
  \((2\mathit{x})\mathit{y}\)
  
  Leave no space between ( and 2.
- between a closing parenthesis, bracket, or brace and the previous character
  
  Example
  
  \(2(\mathit{x}\mathit{y})\)
  
  Leave no space between y and ).
- between back-to-back parentheses, brackets, and braces, e.g., ](
- between nested parentheses, brackets, and braces, e.g., [(

Font

The overall rule is that symbols representing physical quantities or variables are italic (sloping), but symbols representing units, or labels, are roman (upright). Please see specific conventions below:

Use italic type for
- single-letter symbols for variables, physical quantities, and physical constants
  
  Example
  - V
  - P
  For volume and power.
- superscripts and subscripts that are themselves symbols for variables or physical quantities
  
  Example
  
  \(C_{V}\)
  
  For heat capacity at volume V.
Use roman type for
- multiletter variable symbols, mathematical constants, trigonometric functions, mathematical operators, numerals, punctuation, and fences
  
  Example
  - SJW
    
    For Synchronization Jump Width.
  - BRP
    
    For Baud Rate Prescaler.
  - π
  - sin
- superscripts and subscripts that are abbreviations and numbers
  
  Example
  - \(\mathrm{F_s}\)
    
    For sampling frequency. F and s are set in roman.
  - \(t_{\mathrm{Tq}}\)
    
    For time quanta clock cycle. The variable t is set in italic. Tq as abbreviations of time quanta is set in roman.
  - \(πr^2\)
    
    The numeral 2 is set in roman.

Typesetting Formulas

General Typesetting Guidelines

Use parentheses, brackets, and braces appropriately to avoid ambiguity whenever a fraction is unstacked. Both stacking of fractions (i.e., separating numerator and denominator by a horizontal line) and unstacking of fractions (i.e., using a slash in place of the horizontal line) are acceptable as long as clarity is not lost.

Example
- stacked: \(a + \frac{b + c}{d} + e\)
- unstacked: \(a + [(b + c)/d] + e\)
The expression \(a + \frac{b + c}{d} + e\), if written as \(a + b + c/d + e\), is ambiguous and could have several interpretations, such as \(\frac{a + b + c}{d + e}\), or \(a + b + \frac{c}{d} + e\). But its meaning is unambiguous if presented as \(a + [(b + c)/d] + e\).
Enclose parentheses within square brackets, and square brackets within braces.

Note

LaTeX uses {} for grouping and defining arguments for macros, while () are treated as ordinary characters unless specified otherwise. Therefore, in LaTeX, some commands such as the \frac must use curly braces to enclose its arguments, not parentheses.

Example
```
E = 1.96 \left\{ \frac{P(1-P)}{m} \right\}^{1/2}
```
Input the code above in the equation environment in LaTeX, and it will render the formula:

\(E = 1.96 \left\{ \frac{P(1-P)}{m} \right\}^{1/2}\).
In elided lists, commas should come after each term in the list and after the ellipsis points if the list has a final term.

Example

Preferred

Avoid

y = 0, 1, 2, …

y = 0, 1, 2 …

\(x_{1}\), \(x_{2}\), …, \(x_{n}\)

\(x_{1}\), \(x_{2}\), … \(x_{n}\)
Use ending punctuation if equations (whether run in with the text or displayed on a separate line) end a sentence.

Example

If \(a = b\), then for all real numbers \(x\), \(a + x = b + x\).

Use the multiplication sign (×), not the letter x to indicate the mathematical operation.

Example

Preferred	Avoid
\(t_{\mathrm{Tq}}\) = 2 × \(t_{\mathrm{CLK}}\) × (2^{13} × BRP.13 + 2^{12} × BRP.12 + 2^{11} × BRP.11 + … + 2^1 × BRP.1 + 2^0 × BRP.0 + 1)	\(t_{\mathrm{Tq}}\) = 2 x \(t_{\mathrm{CLK}}\) x (2^{13} x BRP.13 + 2^{12} x BRP.12 + 2^{11} x BRP.11 + … + 2^{1} x BRP.1 + 2^{0} x BRP.0 + 1)

How to Type Multiplication Sign
Forms of File	Method
.rst Files	Install the “Insert Unicode” Extension > press `Command + Shift + P` to open the Command Palette > type `Insert Unicode` and select the `Insert Unicode: Insert` command > type `00d7` (the code for multiplication sign) and press `Enter`.
.tex Files	Insert `\times`.
Word Files	Press `Control + Command + Space` to open the Character Viewer > search for “multiplication” in the search bar > click the multiplication sign `×`.

Do not use an asterisk (\(*\)) to indicate multiplication except in computer language expressions.

Example

Preferred

Avoid

\(x_{1}x_{2}\)

\(x_{1}\) \(*\) \(x_{2}\)
Do not use a centered dot (·) or the multiplication sign × with single-letter scalar variables.

Example

Preferred

Avoid

ab

a · b and a × b
Do not use an equal sign as an abbreviation for the word “is” or the word “equals” in narrative text.

Example

Preferred

Avoid

PV = n RT, where P is pressure.

PV = n RT, where P = pressure.

Inline Formulas and Interline Formulas

There are two ways to typeset mathematical formulas: inline formulas and interline (display) formulas.

Inline Formulas

Inline Formulas are integrated within a line of text, which is best for simple equations or symbols or when you want to maintain the flow of text without breaking the paragraph.

In order to fit in with the text, inline formulas appear “cramped” when typesetting large formula elements (fractions, giant operators, etc).

Interline Formulas

Interline formulas are set apart from the text and are centered on their own line. They are typically used for more complex equations or when you want to emphasize a mathematical statement.

Typesetting Inline Formulas in LaTeX

Inline formulas are enclosed by a pair of dollar signs in LaTeX:

$\textrm{LEDC\_CLK\_DIV} = A + \frac{B}{256}$

As for typesetting inline formulas, please note the following guidelines.

Do not wrap inline formulas in parenthesis. Parenthesis are typically used to provide additional information or group related elements. Formulas serve as essential clarification in most cases and therefore should not be enclosed. If it will add confusion to readers, please rearrange the expression and display it apart from the text.

Example

Preferred	Avoid
For chip revision v0.0, the Audio PLL frequency is calculated in hardware as follows: \(f_{\mathrm{out}} = \frac{f_{\mathrm{xtal}} \times (\mathrm{sdm2} + 4)}{2 \times (\mathrm{odiv} + 2)}\).	For chip revision v0.0, the Audio PLL frequency is calculated in hardware as follows: (\(f_{\mathrm{out}} = \frac{f_{\mathrm{xtal}} \times (\mathrm{sdm2} + 4)}{2 \times (\mathrm{odiv} + 2)}\)).

Avoid breaking inline formulas across lines, as it can affect readability. If necessary, rewrite the text or use display mode.

Typesetting Interline Formulas in LaTeX

Interline formulas are wrapped in an equation environment in LaTeX. It automatically generates a number for the equation. If you need to present the formula directly without the number, you can wrap the formula in double dollar signs or \[...\]. See the example below.

With number:

\begin{equation}
    f_{\mathrm{out}} = \frac{f_{\mathrm{xtal}} \left(\mathrm{sdm2} + \frac{\mathrm{sdm1}}{2^8} + \frac{\mathrm{sdm0}}{2^{16}} + 4 \right)}{2 \times (\mathrm{odiv} + 2)}
\end{equation}

Without number:

\[
f_{\mathrm{out}} = \frac{f_{\mathrm{xtal}} \left(\mathrm{sdm2} + \frac{\mathrm{sdm1}}{2^8} + \frac{\mathrm{sdm0}}{2^{16}} + 4 \right)}{2 \times (\mathrm{odiv} + 2)}
\]

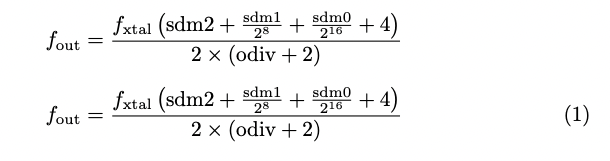
The following figure shows the contrast between formula with number and formula without number.

As for typesetting interline formulas, please note the following guidelines.

Number formulas consecutively if there are numerous equations or if formulas are referred to after initial presentation.
Set numbered equation on a separate line, centered, with parenthetical numbers set flush right.

Citing Formulas in LaTeX

For cross-referencing interline formulas in LaTeX documents, please follow these guidelines:

Wrap interline formulas in an equation environment. This environment automatically generates consecutive numbers for the equations.
Insert \label in the equation environment. Otherwise, the number generated will be the same if different formulas are in the same section. It will cause confusion to formula reference. See the example of adding \label{eq:ledc-clk-float}:
\begin{equation} \textrm{LEDC\_CLK\_DIV} = A + \frac{B}{256} \label{eq:ledc-clk-float} \end{equation}
Use the syntax refer to Equation \ref{label} when referring to the equations. For mathematical expression that does not contain the = symbol, please use Formula (a broader concept) instead of Equation.
Add a word or phrase that describes the nature of the equation when making a reference. For example, “From Equation 1 of LEDC clock” is more helpful than “From Equation 1”.

Provide feedback about this document

Preferred	Avoid
y = 0, 1, 2, …	y = 0, 1, 2 …
\(x_{1}\), \(x_{2}\), …, \(x_{n}\)	\(x_{1}\), \(x_{2}\), … \(x_{n}\)